You seek to make conclusions beyond the immediate facts by using inferential statistics. Inferential statistics, for example, are used to infer what the public would believe based on sample data.

Alternatively, we use inferential statistics to establish whether the difference between groups seen in this study is reliable or random chance.

Inferential Statistics – In a Nutshell

• Inferential statistics aid in the conclusion of an entire population based on a sample of that population.

• Inferential statistics examine a sample to conclude the population, whereas descriptive statistics describe the characteristics of a known dataset.

• There are methods in inferential statistics for verifying and validating our conclusions from an experiment that incorporates hypothesis testing.

• There are three types of hypothesis tests:

• Regression analysis (Simple linear, Multiple linear)

• Tests of comparability (T-test, ANOVA)

• Correlation tests (Chi-square, Pearson's) are used to examine various variables and parameters.

Definition: Inferential statistics

Inferential statistics is a branch of statistics that collects and analyses data using a probabilistic approach.

It enables us to draw inferences and make references about a population based on a sample and apply them to a wider population.

There are numerous forms of inferential statistics, each of which is appropriate for a specific research strategy and sample characteristics.

It is used to compare two models to determine whether one is statistically more significant than the other.

The following statements are clear examples of inferential statistics:

• Based on a survey, the mean weekly hours spent on gaming consoles by teenagers in the United Kingdom is 9.00 hours.

• In 2025, the city b’s population will be 2.5 million.

Descriptive statistics vs. inferential statistics

Descriptive statistics use bar graphs, histograms, or pie charts to organize, summarize, and display the features of a data collection.

They use measures of central tendency such as mean, median, and mode as tools, as well as measures of dispersion and variability such as range, variance, and standard deviation.

Inferential statistics enable us to evaluate hypotheses and determine whether data is generalizable to a larger population.

Sample data is also used to create inferences and draw conclusions about persons, with the results expressed as probabilities.

Inferential statistics: Hypothesis testing

Hypothesis testing is a statistical analysis tool that uses inferential statistics. The goal is to use samples to compare populations across factors.

It consists of the following steps:

1. Determine the null and alternative Hypotheses

The null hypothesis (Ho) asserts that the population's value is considered to be true. The null hypothesis is contradicted by the alternative hypothesis (H1).

It is an educated guess of all eventualities that are not covered by the null hypothesis.

2. Selecting significance level

The criterion by which we judge whether the claim under consideration is true or false.

3. Determine the rejection region

These are the test statistic values for which the null hypothesis is rejected.

The samples are compared, and two decisions are made based on the level of significance. These are some examples:

• Rejecting the null hypothesis: When the null hypothesis is true, the sample average has a low chance of occurrence if the probability of receiving a sample is less than 5%.

• Failure to reject the null hypothesis: When the null hypothesis is true, the sample average has a high likelihood of occurring if the probability of attaining a sample mean is larger than 5%.

Inferential statistical tests are used to test hypotheses, which can be parametric (ANOVA, T-test), which is based on assumptions about the population distribution from which the sample is drawn, or non-parametric (Spearman's correlation), which is not dependent on an assumption.

4. Comparison test

This inferential statistics test determines whether there are discrepancies in the means, medians, or rankings of two or more groups' scores.

5. Correlation test

These inferential statistics tests examine how closely two variables are related.

6. Regression analysis

These inferential statistics tests show whether changes in predictor factors lead to changes in outcome variables.

Inferential statistics example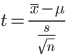

The t-test value can be calculated with the following formula: 

Example:

After new sales training is given to employees, the mean sale goes up to £50 (a sample of 25 employees examined) with a standard deviation of £12. Before the training, the average sale was £100. Check if the training helped at α = 0.05.

Solution: The t-test in inferential statistics solves this problem with the formula:

x = 150, μ = 100, s= 12, n = 25

H0: μ=100

H1: μ=100

= 20.83

The degree of freedom is given by 25 – 1 = 24. Using the t table at α = 0.05, the critical value is T(0.05, 24) = 1.71. As 20.83 > 1.71 thus, H0 is rejected. The conclusion is that the training helped in increasing the average sales.