1)what is the magnetic flux across the surface abcd in the figure?

2)What is the magnetic flux across the surface befc?

3)What is the magnetic flux across the surface aefd?

4)What is the net flux through all five surfaces that enclose the shaded volume?

The magnetic field B in a certain region is 0.128 T, and its direction is that of the z-axis in the Figure (Figure 1) igure 1 of 1 b 30.0 cm 40.0 cm 30.0 cm a f -x 50.0 cm d

Part A.

We know that magnetic flux is given by:

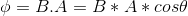
B = Magnetic field = 0.128 T

A = Area of surface abcd = 40.0 cm*30.0 cm = 0.12 m^2

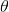 = Angle between Area vector and magnetic field = 90 deg (Since Area vector is in -ve x-direction and magnetic field is in +z-direction), So

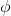 = 0.128*0.12*cos 90 deg

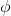 = 0 Wb

Part B.

We know that magnetic flux is given by:

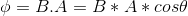
B = Magnetic field = 0.128 T

A = Area of surface befc = 30.0 cm*30.0 cm = 0.09 m^2

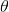 = Angle between Area vector and magnetic field = 180 deg (Since Area vector is in -ve z-direction and magnetic field is in +z-direction), So

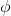 = 0.128*0.09*cos 180 deg

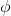 = -0.01152 Wb = -0.0115 Wb

Part B.

We know that magnetic flux is given by:

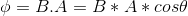
B = Magnetic field = 0.128 T

A = Area of surface aefd = 50.0 cm*30.0 cm = 0.15 m^2

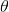 = Angle between Area vector and magnetic field = arccos (3/5)

cos 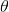 = 3/5

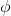 = 0.128*0.15*(3/5)

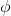 = 0.01152 Wb = 0.0115 Wb

Part D.

magnetic flux through abe and cdf will be zero because both have 90 deg angle between area vector and magnetic field, So

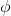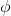 =  _abcd +  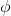_befc +  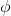_aefd +  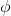_abe +  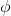_cdf

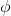 = 0 - 0.01152 + 0.01152 + 0 + 0

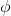 = 0 Wb