13) AZIZ Corporation has prepared the following information regarding two investments under consideration. Calculate the expected rate of return and standard deviation. Which investment should be accepted? Chell Betronas Probability 0.2 0.4 12 percent 10 percent 15 percent 5 percent 12 percent 17 percent 11 percent 14 percent 0.1 0.3 a) Calculate the expected return for Chell and Bet b) Calculate the standard deviation for Chell and Betronas c) Calculate the CV (coefficient of variation) d) Based on your answer, which stock should you select and why? 14.Given the following information about Asset A and Asset B. Probability Asset A Asset B 0.30 15 percent 20 percent 0.40 9 percent 5 percent 0.30 18 percent 12 percent a) Calculate the expected return and standard deviation for both of the asset b) Calculate the CV (coefficient of variation) c) Based on your answer, which stock should you choose?

13.

Probability	Chell	Betronas
0.2	12%	12%
0.4	10%	17%
0.1	15%	11%
0.3	5%	14%

a)

Probability	Return of Chell	Probability * Return of Chell
0.2	12%	2.4%
0.4	10%	4.0%
0.1	15%	1.5%
0.3	5%	1.5%

Expected return of Chell = 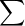 Probability * Return of Chell

Expected return of Chell = 2.4 + 4 + 1.5 + 1.5

Expected return of Chell = 9.4%

Probability	Return of Betronas	Probability * Return of Betronas
0.2	12%	2.4%
0.4	17%	6.8%
0.1	11%	1.1%
0.3	14%	4.2%

Expected return of Betronas = 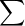 Probability * Return of Chell

Expected return of Betronas = 2.4 + 6.8+ 1.1 + 4.2

Expected return of Betronas = 14.5%

b)

Chell

Probability	Return	Return - Mean (9.4)	(Return - Mean)^2	[(Return - Mean)^2 * Probability]
0.2	12%	2.6%	0.000676	0.0001352
0.4	10%	0.6%	0.000036	0.0000144
0.1	15%	5.6%	0.003136	0.0003136
0.3	5%	-4.4%	0.001936	0.0005808

Variance of Chell = 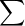 [(Return - Mean)^2 * Probability]

Variance of Chell = 0.0001352 + 0.0000144 + 0.0003136 + 0.0005808

Variance of Chell = 0.001044

Standard deviation of Chell = Square root (Variance of Chell)

Standard deviation of Chell = Square root (0.001044)

Standard deviation of Chell = 0.032311 = 3.231%

Betronas

Probability	Return	Return - Mean (14.5)	(Return - Mean)^2	[(Return - Mean)^2 * Probability]
0.2	12%	-2.5%	0.000625	0.000125
0.4	17%	2.5%	0.000625	0.00025
0.1	11%	-3.5%	0.001225	0.0001225
0.3	14%	-0.5%	0.000025	0.0000075

Variance of Betronas = 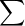 [(Return - Mean)^2 * Probability]

Variance of Betronas  = 0.000125 + 0.00025 + 0.0001225 + 0.0000075

Variance of Betronas = 0.000505

Standard deviation of Betronas = Square root (Variance of Betronas)

Standard deviation of Betronas = Square root (0.000505)

Standard deviation of Betronas = 0.0224722 = 2.247%

c)

CV of Chell = Standard deviation of Chell / Expected return of Chell

CV of Chell = 3.231% / 9.4%

CV of Chell = 0.3437

CV of Betronas = Standard deviation of Betronas / Expected return of Betronas

CV of Betronas = 2.247% / 14.5%

CV of Betronas = 0.15498

d)

AZIZ Corporation must select investment Betronas, since the coefficient of variation of Betronas is less than that of Chell, which indicates that Betronas is more stable as compared to Chell as the risk assumed for per unit of its expected return is less for Betronas (0.15498) as compared to Chell (0.3437).

Hence, Betronas is a better option.

14.

Probability	A	B
0.3	15%	20%
0.4	9%	5%
0.3	18%	12%

a)

Asset A

Probability	Return	Return * Probability	Return - Mean (13.5)	(Return - Mean)^2	[(Return - Mean)^2 * Probability]
0.3	15%	4.5%	1.5%	0.000225	0.0000675
0.4	9%	3.6%	-4.5%	0.002025	0.00081
0.3	18%	5.4%	4.5%	0.002025	0.0006075

Expected return of Asset A = 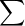 Probability * Return of Chell

Expected return of Asset A = 4.5 + 3.6 + 5.4

Expected return of Asset A = 13.5%

Variance of Asset A = 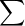 [(Return - Mean)^2 * Probability]

Variance of Asset A = 0.0000675 + 0.00081 + 0.0006075

Variance of Asset A  = 0.001485

Standard deviation of Asset A = Square root (Variance of Asset A)

Standard deviation of Asset A = Square root (0.001485)

Standard deviation of Asset A = 0.0385357 = 3.854%

Asset B

Probability	Return	Return * Probability	Return - Mean (11.6)	(Return - Mean)^2	[(Return - Mean)^2 * Probability]
0.3	20%	6.0%	8.4%	0.007056	0.0021168
0.4	5%	2.0%	-6.6%	0.004356	0.00174
0.3	12%	3.6%	0.4%	0.000016	0.0000048

Expected return of Asset B = 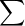 Probability * Return of Chell

Expected return of Asset B = 6 + 2 + 3.6

Expected return of Asset B = 11.6%

Variance of Asset B = 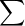 [(Return - Mean)^2 * Probability]

Variance of Asset B = 0.0021168 + 0.00174 + 0.0000048

Variance of Asset B = 0.003864

Standard deviation of Asset B = Square root (Variance of Asset B)

Standard deviation of Asset B = Square root (0.003864)

Standard deviation of Asset B ???????= 0.062161 = 6.216%

b)

CV of Asset A = Standard deviation of Asset A / Expected return of Asset A

CV of Asset A  = 3.854% / 13.5%

CV of Asset A  = 0.2854

CV of Asset B = Standard deviation of Asset B / Expected return of Asset B

CV of Asset B = 6.216% / 11.6%

CV of Asset B = 0.5359

c)

One must select Asset A, since the coefficient of variation of Asset A is less than that of Asset B, which indicates that Asset A is more stable as compared to Asset B as the risk assumed for per unit of its expected return is less for Asset A (0.2854) as compared to Asset B (0.5359).

Hence, Asset A??????? is a better option.