question archive The time to complete an exercise for a particular class follows an exponential distribution with lambda = 1/60 min-1 (λ = 1 /60min) What is the expected time to complete an exercise for this class? What is the variance in the time to complete an exercise for this class? You take a random sample of 100 exercises taken for this class
The time to complete an exercise for a particular class follows an exponential distribution with lambda = 1/60 min-1 (λ = 1 /60min) What is the expected time to complete an exercise for this class? What is the variance in the time to complete an exercise for this class? You take a random sample of 100 exercises taken for this class
Subject:MarketingPrice:2.87 Bought7
The time to complete an exercise for a particular class follows an exponential distribution with lambda = 1/60 min-1 (λ = 1 /60min)
What is the expected time to complete an exercise for this class?
What is the variance in the time to complete an exercise for this class?
You take a random sample of 100 exercises taken for this class. What is the expected mean time to complete the exercise for your random sample of 100 exercises?
What is the standard error of the mean time to complete the exercise for your random sample of 100 exercises?
What is the probability that your sample mean time to complete the exercises is greater than 70 minutes?
What is the interquartile range of sample mean time to complete the exercise?
Purchase A New Answer
Custom new solution created by our subject matter experts
GET A QUOTE
Answer Preview
Answer:
Here given is The time to complete an exercise for a particular class follows an exponential distribution with lambda = 1/60 min-1 λ = 1 /60min
(a) Expected time to complete an exercise for this class = 1/λ = 1/(1/60) = 60 mins
(b) Variance in the time to complete an exercise for this class = 1/λ2 = 602 = 3600 mins2
(c) Here sample size = n = 100
as the sample size is greater than 30 so from central limit theorem we can say that the distribution of the sample would be approximately normal where
mean = 60 mins and variance = 3600/100 = 36
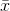~ NORMAL (60 mins, 36 mins2)
standard error = sqrt(36) = 6 mins
(d) Here we have to find
P(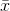 > 70) = 1 - P( 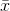< 70)
z = (70 - 60)/6 = 1.6667
P(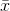 > 70) = 1 - NORMSDIST(1.6667) = 1 - 0.9522 = 0.0478
(e) Here for interquartile range, percentile is 75 and 25 th
z value for 75th percentile = NORMSINV(0.75) = 0.6745
z value for 25th percentile = NORMSINV(0.25) = -0.6745
75th percentile = 60 + 6 * 0.6745 = 64.05 mins
25th percentile = 60 - 6 * 0.6745 = 55.95 mins
Interquartile range = 64.05 - 55.95 = 8.10 mins
